Pythagoras Pythagoras' Theorem says that for a right angled triangle, the square of the long side equals the sum of the squares of the other two sides x 2 y 2 = 1 2 But 1 2 is just 1, so x 2 y 2 = 1 (the equation of the unit circle) Also, since x=cos and y=sin, we get (cos(θ)) 2 (sin(θ)) 2 = 1 a useful "identity" Important Angles 30°, 45° and 60° You should try to rememberDetermine angle type 240 is an obtuse angle since it is greater than 90° tan (240) = √ 3 In Microsoft Excel or Google Sheets, you write this function as =TAN (RADIANS (240)) Important Angle Summary θ° θ radians= 1 / 2√3 = (1 / 2√3) x (2√3 / 2√3) So, cot 15 0 = 2 √3 So, on putting the values of cot 15 0 and tan 15 0 in equation (i), we will get = (2 √3) 2 (2 √3) 2 = 4 3 2√3 4 3 2√3 = 14

Find The Square Root Of X 2 9 9 4x 2 X 3 3
3 2 1 24kgoldn lyrics
3 2 1 24kgoldn lyrics-K O T P C T ?Matemática com baya April 23 · As medidas dos lados de um triângulo são exoressas por x1;2x;




View Question Square Root 3 2 1 2 150 Degrees 5pie 6
Simplify 1/2√3 2/√5√3 1/2√5 Maths NCERT Solutions;Mathx = \dfrac{\sqrt{31}}{2} \tag {E01}/math math\implies 2x = \sqrt{3}1 \implies (2x1) = \sqrt{3} \tag {E02} /math math\text{Squaring }(2x1)^2 = 3 If sin1 x cot1 (1/2) = π/2, then x is equal to (a) 1/2 (b) 1/√5 (c) 2/√5 (d) √3/2 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries
√3)/2 = is a nonterminating and nonrecurring decimal and therefore is an irrational number (B) (√2 √3)/2 Exercise 12 Page No 6 1 Let x and y be rational and irrational numbers, respectively Is x y necessarily an irrational numberIf tanθ=√(3/2), then sum of the infinite series 12(1cosθ)3〖(1cosθ)〗^24〖(1cosθ)〗^3 ∞ is (a) 2/3 (b) √3/4 (c) 5/(2√2) (d) 5/2To buy(x^2) 5 e estão em PA,nesta ordemDetermine o perimetro do mesmo triângulo Measures on the sides of a triangle are exorced by x 1;2 x;
Ex 33, 5Find the value ofsin 75°sin 75° = sin (45° 30°) = sin 45° cos 30° cos 45° sin 30° = 1/√2 × √3/2 1/√2 × 1/2 = 1/√2 (√3/2 " " 1/2) = (√𝟑 𝟏)/(𝟐√𝟐) sin (x y) = sin x cos y cos x sin yPutting x = 45° and y = 30°Ex 33, 5Find the value of3 Chapter 1 c2 1 2 ( √ 3 ) 2 4 ⇒ c √ 4 2 d2 1 2 2 2 5 ⇒ d √ 5 e2 1 2 (√ 5 ) 2 6 ⇒ e √ 6 f 2 1 2 ( √ 6 ) 2 7 ⇒ f √ 7 g2 1 2 ( √ 7 ) 2 8 ⇒ g √ 8 2 √ 2 The length of "c" is a rational number 13 Since the length of the carpet equals the sum of the heightWrite sin (81) in terms of cos Since 81° is less than 90, we can express this in terms of a cofunction sin (θ) = cos (90 θ) sin (81) = cos (90 81) sin (81) = cos (9) In Microsoft Excel or Google Sheets, you write this function as =SIN (RADIANS (81))




If N Square Root 3 2 2 Square Root 3 2 2 Square Root 3 1 2 Square Root 3 1 Then N Equal To 1 Maths Number Systems Meritnation Com
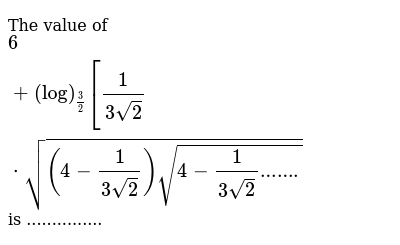



The Value Of 6 Log 3 2 1 3sqrt 2 Sqrt 4 1 3sqrt 2
Next consider 30° and 60° angles In a 30°60°90° right triangle, the ratios of the sides are 1 √3 2 It follows that sin 30° = cos 60° = 1/2, and sin 60° = cos 30° = √3 / 2 Prove that (i) tan 225 ° cot 405 ° tan 765 ° cot 675 ° = 0 (ii) sin 8π/3 cos 23π/6 cos 13π/3 sin 35π/6 = 1/2 (iii) cos 24 ° cos 55 ° cos 125 ° cos 4 ° cos 300 ° = 1/2 (iv) tan (125 °) cot (405 °) – tan (765 °) cot (675 °) = 0 (v) cos 570 ° sin 510 ° sin (330 °) cos (390 °) = 0 (vi) tan 11π/3 – 2 sin 4π/6 – 3/4 cosec 2 π/4 4 cos 2 17π/6Calculate cos(16)° Determine quadrant Since our angle is between 0 and 90 degrees, it is located in Quadrant I In the first quadrant, the values for sin, cos and tan are positive




Log X Square Root Of 1 27 3 2 X Cx 25 Gauthmath




Find The Square Root Of X 2 9 9 4x 2 X 3 3
Sin(15) cos(15) = sin(45 30) cos(45 30) = sin(45)cos(30) cos(45)sin(30) cos(45)cos(30) sin(45)sin(30) = (1/√2)(√3/2) (1/√2)(1/2) (1/√2)(√3>Sequences and series > Geometric progression Geometric progression > 1 √(2)12 (3) 3 2√(2) 1 √(2)12 (3) 3 2√(2)(x ^ 2)5 and are in P A, in this order Determine the perimeter of the same triangle Translated 6



Answered The Graph Of Y Vt Is Given Below 4 Bartleby




Eq 11 The Higher Curve And The Square Root Of Eq 10 The Lower Download Scientific Diagram
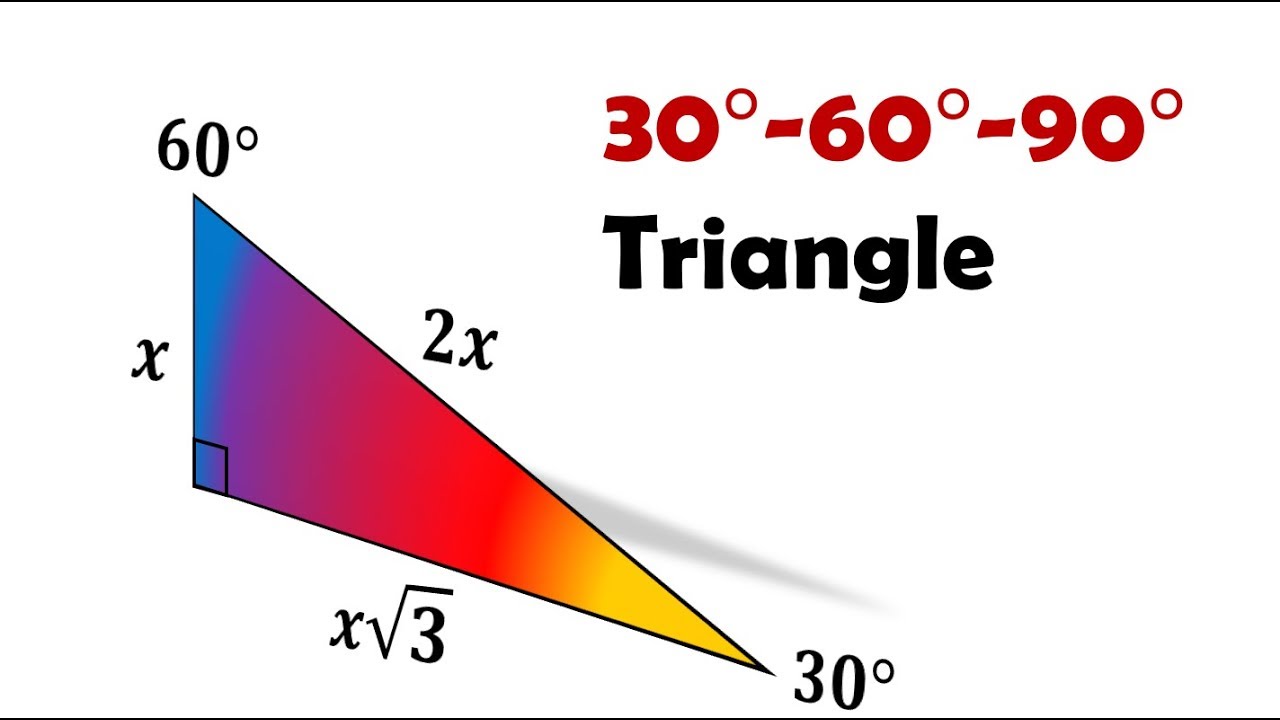
So if you recall, the short leg is 1/2 the hypotenuse, so the ycoordinate is 1/2, and the long leg is √3 times the shorter leg, or (√3)/2, so the xcoordinate is (√3)/2 The coordinates of that point are ((√3)/2,1/2) Now use the identities in the previous step to find thatA special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist For example, a right triangle may have angles that form simple relationships, such as 45°–45°–90° This is called an "anglebased" right triangle A "sidebased" right triangle is one in which the lengths of the sides form ratios ofP C T 0° 0 0 1 0 − 30° π 6 1 2 √3 2 √3 3 √3 45° π 4 √2 2 √2 2 1 1 60° π 3 √3 2 1 2 √3




Simplify 1 2 3 2 5 3 1 2 5 Brainly In




Solving Quadratic Equations By Square Root Method By
If P = (√3/2, 1/2), (1/2, √3/2), A = (1, 1), (0, 1) and Q = PAPT, then PTQ05 P is Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries If i =√1, then 4 5(1/2 i√3/2)334 3(1/2 i√3/2)365 is equal to (a) 1 i√3 (b) 1 i√3 (c) i√3 (d) i√3We thoroughly check each answer to a question to provide you with the most correct answers Found a mistake?




Solved If X 3 2 2 Check Whether X 1x Is Rational Or Irrational Self Study 365




2 4 1 3 3 14 7 6 3 2 1 2 2 3 Gauthmath
If x = 1/(2 − √3), find the value of x3 − 2x2 − 7x 5 Let us first rationalise x x = 1/(2 − √3) = 1/(2 − √3) × (2 √3)/(2 √3) = (2 √3)/(2We take (2√3) = a equation (2√3) = b equation In a equation we take 2 and Multiply by equation b * (2)×(2√3) Then we multiply 2 by 2 and then 2 by √3 " in above equation" * 2×2 = 4 * 2×√3 = 2√3 Then we add the above equationLet us know about it through the REPORT button at the bottom of the page Click to rate this post!




If X 2 Root 3 Find The Value Of X 1 X Whole Cube Brainly In




How To Find 1 2 Of 2 3 Video Lesson Transcript Study Com
Chapter 6 – Polar System Answer Key CK12 Trigonometry Concepts 23 611 Quotient Theorem Answers 1 3 2 (cos17°𝑖sin17°) 2 1 5 (cos358°𝑖sin358°) 3 1 2 (cos343°𝑖sin343°)The value of 1/2√33/√6√32/2√6 dhairyaviramgami007 is waiting for your help Add your answer and earn pointsThe value of {(√√3 1 √√3 1)^2 (√3 √2)} / (√√3 1)^2 (√√3 1)^2 is



Express Each One Of The Following With Rational Denominator I 1 3 2 Ii 1 6 5 Iii 16 41 5 Sarthaks Econnect Largest Online Education Community



Rationalise The Denominator Of 1 3 2 And Hence Evaluate By Taking 2 1 414 And 3 1 732 Up To Three Places Of Decimal Studyrankersonline
P = ( 1/2 , 1 − √3/2) , Q = ( 1 − √3/2 , 1/2) These points lie on the circle with centre (1, 1) and radius 1 Show that this circle defines a straight line in the Poincar´e disc model of the Hyperbolic Plane (Hint sketch this circle) Use this information to find the hyperbolic distance d(P, Q)First solve the inside bracket value 2 c o s − 1 2 3 The range of the principal value of c o s − 1 x is 0, π Let c o s − 1 2 3 = x c o s x = 2 3 x = 6 π where x ∈ 0, π 2 c o s − 1 2 3 = 2 6 π = 3 π Then the expression reduces to t a n − 1 (2 s i n 3 π ) Now we are going to reduce the term 2 s i n 3 π We know that s i n 3Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



Prove Side Ratios For 30 60 90 Triangle 1 Sqrt 3 2 Youtube




How To Do This Question X 3 1 2 Find Value Of 4x 3 2x 2 8x 7 Mathematics Topperlearning Com 4r5prjll
) = (−1 2,√3 2) ดังนั้นcosec 2𝜋 3 = 2 √3 sec 2 3 = −2 1 = −2 tan 2𝜋 3 = √3/2 −1/2 = −√ u cot 2𝜋 3 = −1/2 √3/2 = −1 √3 เป็นต้น หมายเหตุ cot𝜃 กับ cosec𝜃 จะหาค่าไม่ได้ เมื่อ sin𝜃 = 0If x = 2√3 find the value of x31x3 Given x=2√31x=12√3x1x=2√312√3x1x=2√32√312√3 by taking LCMx1x=2√3212√3x1x=22√322×2×√312√3In this explainer, we will learn how to determine whether a matrix is orthogonal and how to find its inverse if it is In linear algebra, there are many special types of matrices that are interesting either because of the geometric transformations that they represent, or because of the convenient algebraic properties that they hold




Int X 3dx Sqrt 1 X 2 Is Equal To A 1 3sqrt 1 X 2 2




Prove That 1 2 Root 3 2 Root5 Root 3 1 2 Root 5 Brainly In
𝑟2cos2𝜃𝑟2sin2𝜃=(−√3) 2 12 ⇒𝑟2=31=4 cos2𝜃sin2𝜃=1 ⇒𝑟=√4=2 Conventionally, 𝑟>0 Therefore, Modulus =2 Step2 ∴2cos𝜃=−√3and 2sin𝜃=1 ⇒cos𝜃=−√3 2 and sin𝜃=1 2 Therefore, 𝜃=𝜋−𝜋 6 =5𝜋 6 As 𝜃 Example If A = 8(3&√3&2@4&2&0) and B = 8(2&−1&2@1&2&4) Verify that (i) (A')' = A, A = 8(3&√3&2@4&2&0) A' = 8(3&√3&2@4&2&0)^′= 8(3&4Class XICBSEMathematics Polynomials Practice more on Polynomials Page 4 wwwembibecom (ii) Linear, quadratic, cubic polynomials have its degree 1, 2, 3 respectively



Express Each One Of The Following With Rational Denominator I 1 3 2 Ii 1 6 5 Iii 16 41 5 Sarthaks Econnect Largest Online Education Community
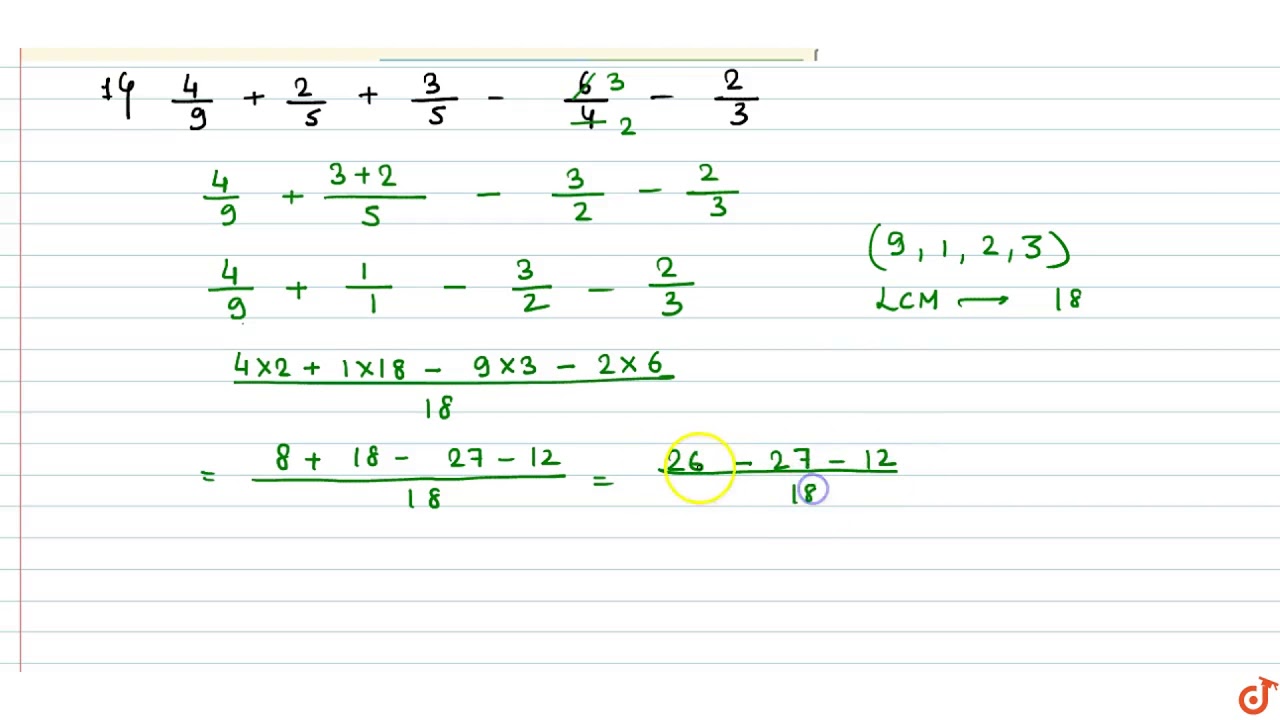



Simplify The Expressions 1 4 9 2 5 3 5 6 4 2 3 2 11 2 8 3 4 2 5 Youtube
Total 133 Average 24 Questions and Answers to Learn 1) Based on your unit circle cos(0o)= Unit Circle Quiz Practice Read More »Learn unit circle with free interactive flashcards Choose from 500 different sets of unit circle flashcards on QuizletCot(21) = Write cot(21) in terms of tan Since 21° is less than 90, we can express this in terms of a cofunction cot(θ) = tan(90 θ)




How Sin 60 Is Equal To 3 2 Quora



Rationalise The Denominator In Each Of The Following And Hence Evaluate By Taking 2 1 414 3 1 732 And 5 2 236 Up To Three Places Of Decimal Studyrankersonline
Ex 81, 9 In triangle ABC, rightangled at B, if tan A = 1/√3, find the value of sin A cos C cos A sin C tan A = 1/√3 (𝑠𝑖𝑑𝑒T grade T radiani O E J T ? For the principal values, evaluate each of the following sin^1(1/2) 2 cos^1(√3/2) asked Mar in Trigonometry by Yaad ( 352k points) inverse trigonometric functions




Square Root Of 2 Wikipedia




1 1 2 1 2 3 1 3 4 1 4 5 1 5 6 1 6 7 1 7 8 1 8 9 2 Mathematics Topperlearning Com Lbve3ydd
Click here👆to get an answer to your question ️ Simplify 1/1 √(2) 1/√(2)√(3) 2/√(3)√(5)




For A Complex Number 1 2 J Square Root 3 2 Find Chegg Com
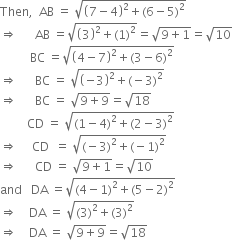



Name The Type Of Quadrilateral Formed If Any By The Following Points And Give Reasons For Your Answer 4 5 7 6 4 3 1 2 From Mathematics Coordinate Geometry Class 10 Cbse




Square Root Of 2 Wikipedia




Mathematics Class 9th Chapter 2 Solution




Chapter 7 Radicals Radical Functions And Rational Exponents Ppt Video Online Download




3 2 1 2 5 3 Rationalise This Term In Briefly Brainly In




Some Fun With Counting In Logistics And The Square Root Law Of Distribution Cost
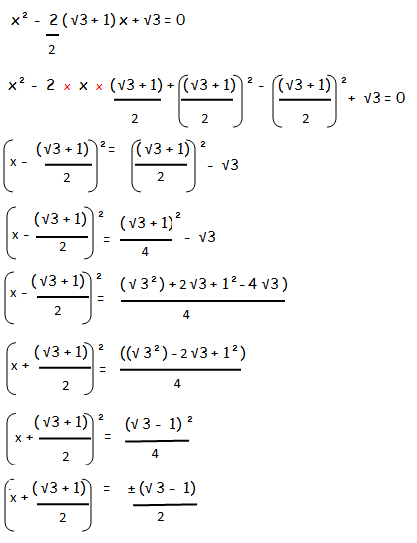



Complete The Square




Simplify 1 1 2 1 2 3 1 3 4 Brainly In




Square Root Of Frac216 2 3 25 1 2 1 25 3 2 Gauthmath
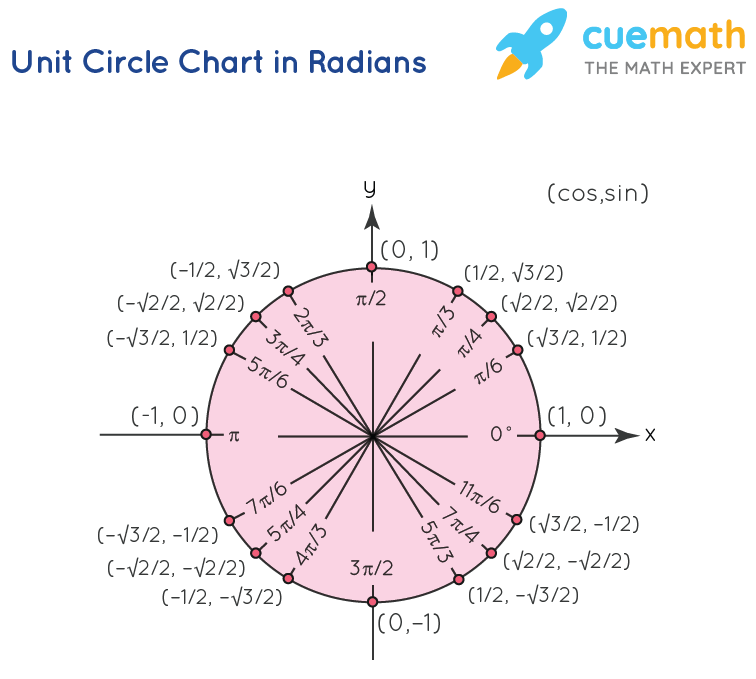



Unit Circle Equation Of A Unit Circle Unit Circle Chart



What Is The Value Of 3 2 2 Quora



Free Math Answers Answers Within 24 Hours Step By Step Explanations




Rd Sharma Solutions For Class 11 Maths Chapter 13 Complex Numbers Download Free Pdf
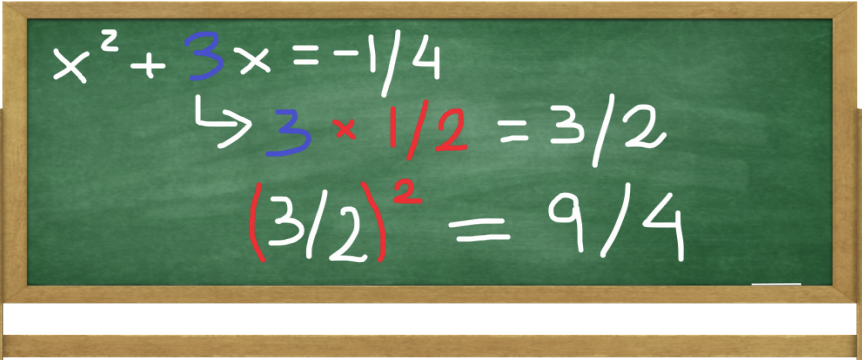



Completing The Square Formula How To Complete The Square With A Quadratic Equation




Relationship Of The Diffusion Thickness H And The Square Root Of Download Scientific Diagram




Rd Sharma Solutions For Class 11 Maths Chapter 13 Complex Numbers Download Free Pdf




Wolfram Alpha Examples Step By Step Solutions




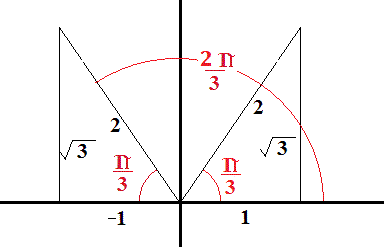
Ex 2 1 7 Find Principal Value Of Sec 1 2 Root 3 Chapter 2




Ex 1 6 3 Simplify I 2 2 3 2 1 5 Ii 1 33 7 Ex 1 6




Extract The Square Root Of A 2 Left Frac Left 3a Sqrt A Right 2 Right Left Frac Left 3 Sqrt A Right 2 Right Frac 41a 16 1 Mathematics Stack Exchange




Simplify 2 5 3 1 3 2 3 5 2



What Is The Sin 1 Sqrt 3 2 Socratic



1




Aim How Do We Handle Fractional Exponents Do




How To Solve 1 1 2 2 3 Quora



How To Rationalise The Denominator 1 2 3 5 Quora




If X Radic 3 1 2 Then The Value Of X2 1 X2 And X2 Ndash 1 X2 Mathematics Topperlearning Com Vdywlvdd




Integral 2x 3 2 1 4x 4 6 Dx Integral Chegg Com




Mathematics Class 9th Chapter 2 Solution




Is There A Solution For X For X 2 Y Sqrt 3 X 2 2 1 Mathematics Stack Exchange



Plos One Heart Rate Variability In Type 2 Diabetes Mellitus A Systematic Review And Meta Analysis



Q Tbn And9gcsb2rnpibjsemfefshm1leviszzhattq67fri0obpzhq J Lxfh Usqp Cau




Some Fun With Counting In Logistics And The Square Root Law Of Distribution Cost



If X 3 2 2 Then What Is The Value Of X 1 X Quora



Bisection Method
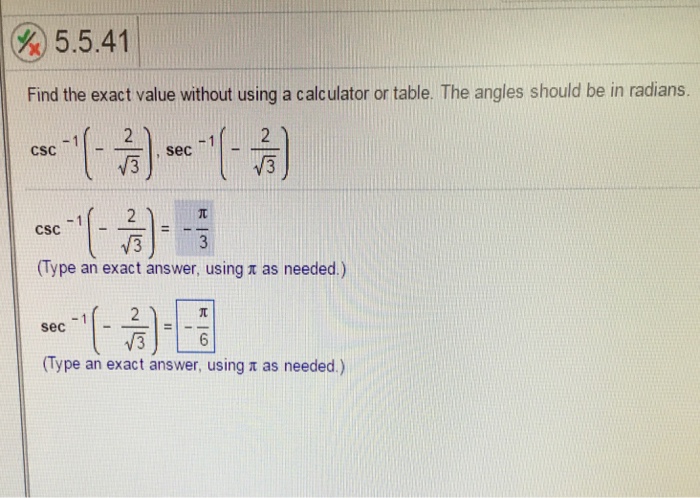



What Is The Answer To Sec 1 2 Square Chegg Com




If X 3 2 2 Then Check Whether X 1 X Is Rational Or Irrational Cbse Class 9 Maths Learn Cbse Forum




Square Root 2 3 Cannot Be Equal 1 3 1 2 2 6 2 2 3 2 3 1 4 3 1 2 Maths Number Systems Meritnation Com
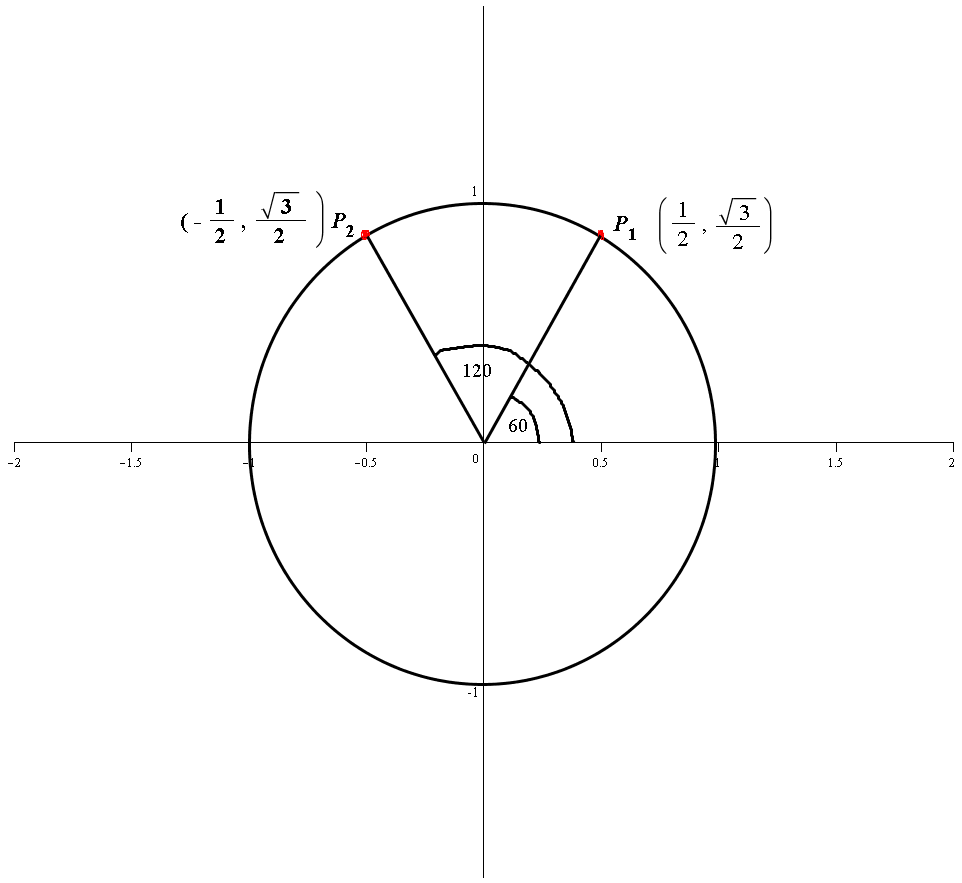



If The Point X Sqrt 3 2 Is On The Unit Circle What Is X Socratic



Frac Square Root Of 1 3 4 Cube Root Of 2 3 1 Gauthmath




Find The Sum 1 1 Sqrt 2 1 Sqrt 2 Sqrt 3 1 Sqrt 3 Sqrt 4 Youtube




Simplify I 1 3 2 1 2 3 1 4 2 Ii
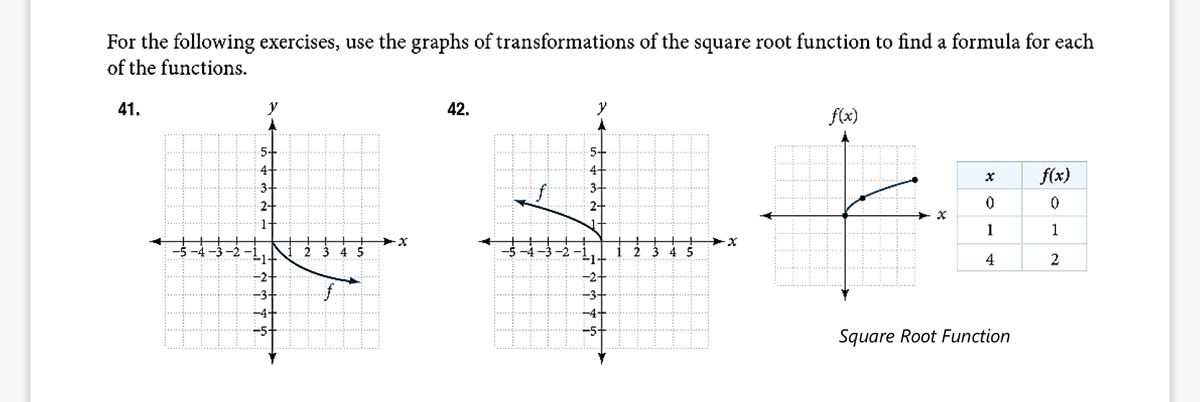



Answered 41 42 F X F X 3 2 1 1 1 1 4 1 Bartleby



If X 3 2 2 Then What Is The Value Of X 1 X Quora
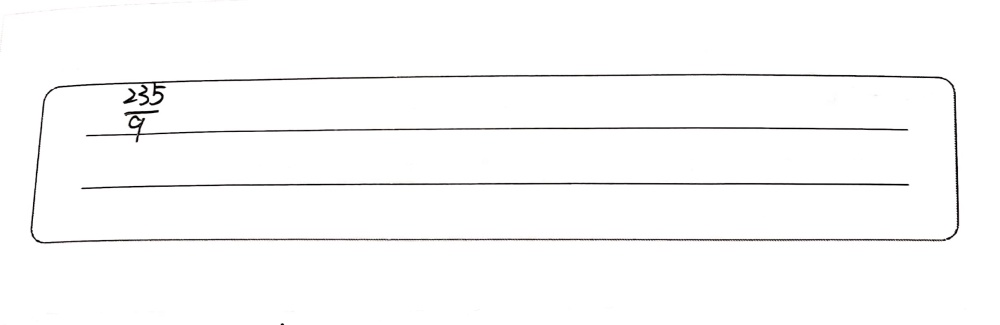



R Frac 1 8 1 3 3 2 2 Square Root Of 12 Gauthmath




Square Root Of 2 Wikipedia
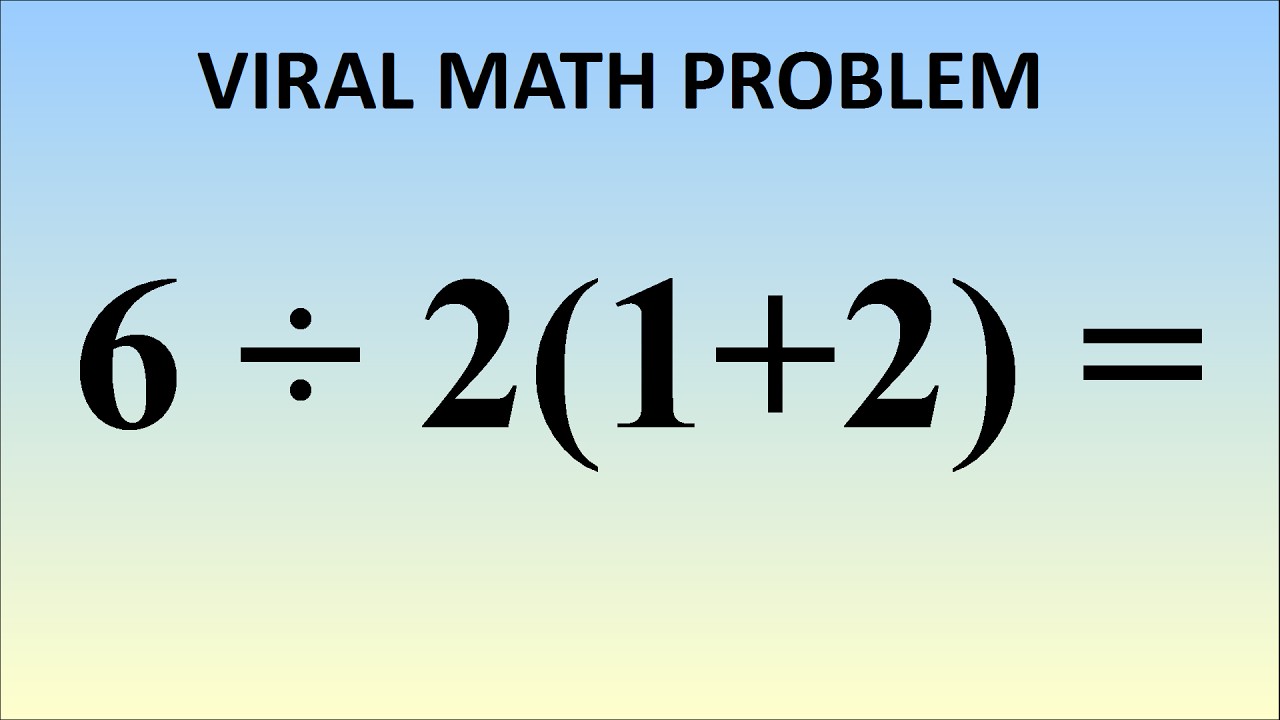



6 2 1 2 Mathematician Explains The Correct Answer Youtube




Ex 2 1 14 Find Value Of Tan 1 Root 3 Sec 1 2 Ex 2 1



1




Unit 5 Radicals And Equations Of A Line Ppt Download
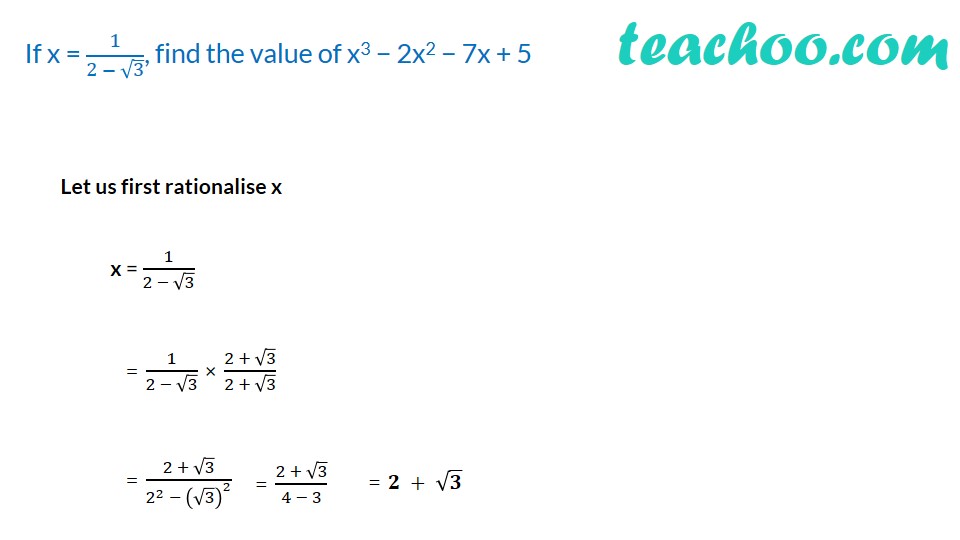



If X 1 2 3 Find The Value Of X 3 2x 2 7x 5 Video T




If X 1 2 3 Find The Value Of X 3 2x 2 7x 5 Video T




Multiplying And Dividing Radical Expressions




What Is The Solution Of 2 3 2 3 Quora



If I 1 Then 4 5 1 2 I 3 2 334 3 1 2 I 3 2 365 Is Equal To Sarthaks Econnect Largest Online Education Community



View Question Square Root 3 2 1 2 210 Degrees 7pie 6 Find Sin Cos Tan Cot Csc And Sec




If X 3 2 2 Find X 4 1x 4




Multiplying And Dividing Radical Expressions




If X 3 2 2 Find X 3 1 X3 Brainly In



Q Tbn And9gcrdpezo9dtgnwo1evsbut2dx1dc1fff 52tf0 Uifj9lvz9 Uby Usqp Cau




Introduction To Complex Numbers And Complex Solutions




A 3 2 2 Then The Value Of A 1 2 A 1 2 Can Foundation Brainly In




Rationalize The Denominator 1 2 3 7 And 2 1 3 5 2 2 Brainly In




Square Root Of 3 Wikipedia




A Cambridge Interview Problem Sqrt 3 2sqrt 2 Youtube




View Question Square Root 3 2 1 2 150 Degrees 5pie 6




4 The Square Root Of 3 Sqrt 5 Is A Sqrt 3 2 1 Sq



What Is The Principal Value Of Cos 1 3 2 Sarthaks Econnect Largest Online Education Community




Rationalize The Denominator Of 1 3 2 Under Root 2 Under Root 5 Mathematics Topperlearning Com 8pvu0x66




A Write If The Square Root Of See How To Solve It At Qanda




Maximum Value Of Function F X Frac X 4 X 2 X 6 2x 3 1 When X 1 Mathematics Stack Exchange




Multiplying Complex Numbers Video Khan Academy




Example 18 Rationalize The Denominator Of 1 2 Root 3
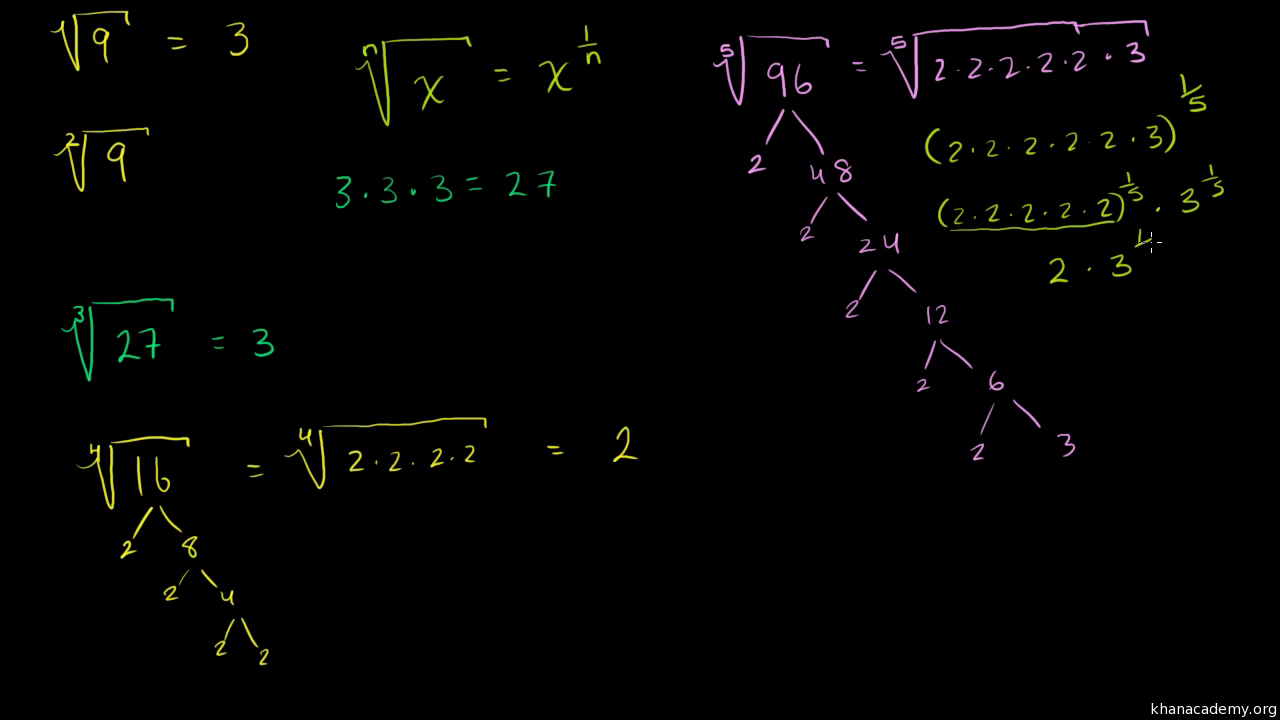



Simplifying Higher Index Roots Algebra Video Khan Academy




Rationalise The Denominator Of 1 2 Sqrt 3 Youtube
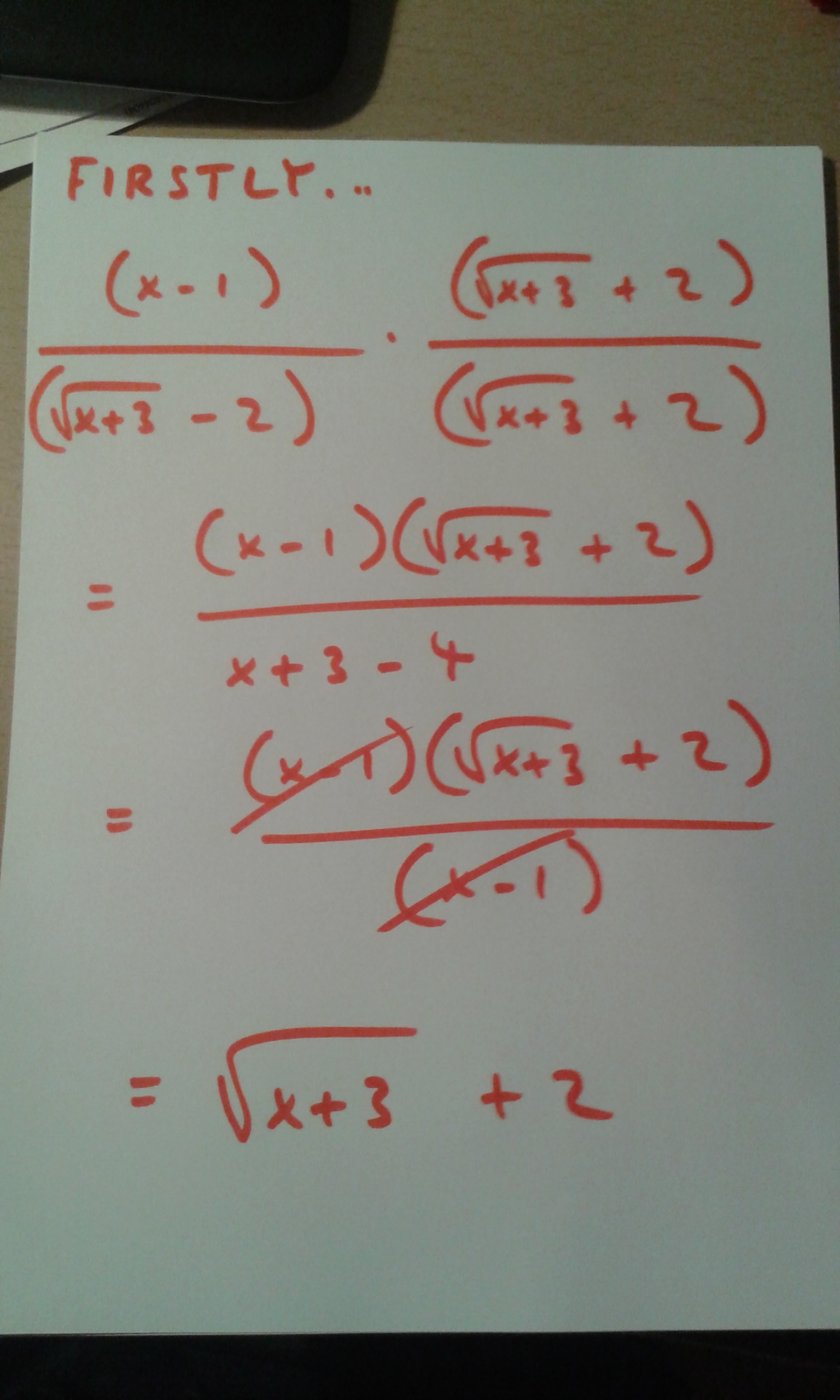



How Do You Find The Limit Of X 1 Sqrt X 3 2 As X Approaches 1 Socratic




Doc Archimedes Square Root Of 3 5 6 7 And 29 Milo Gardner Academia Edu



If X 3 2 2 Then What Is The Value Of X 1 X Quora
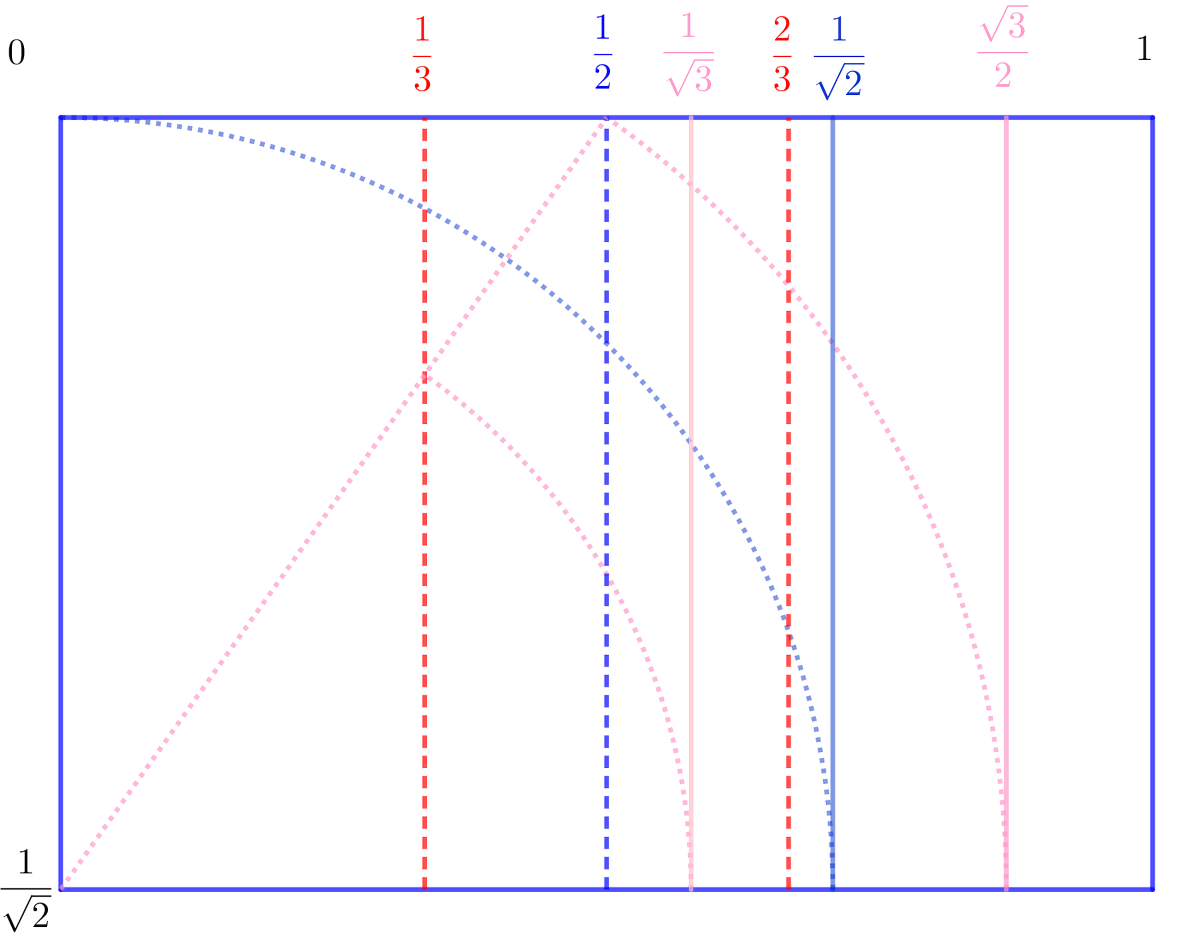



Christian Mercat And What Is A The Root Of Thirdsday Well The Inverse Of The Square Root Of 3 Day Which Is Easily Drawn On An Paper Reminding


