底面積 は、半径5cmの円の面積2つ分なので、 \pi×5^2×2=50\pi (cm^2) π × 52 × 2 = 50π(cm2) 側面積 は、縦の長さ9cm、横の長さ2π×5 (cm)の長方形なので、 9×2\pi×5=90\pi (cm^2)H:高さ C円錐体形鏡板(Conical)Type A ごA = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積
球の表面積 アルキメデスの方法 4の2 セルフ塾のブログ
円錐の面積の出し方
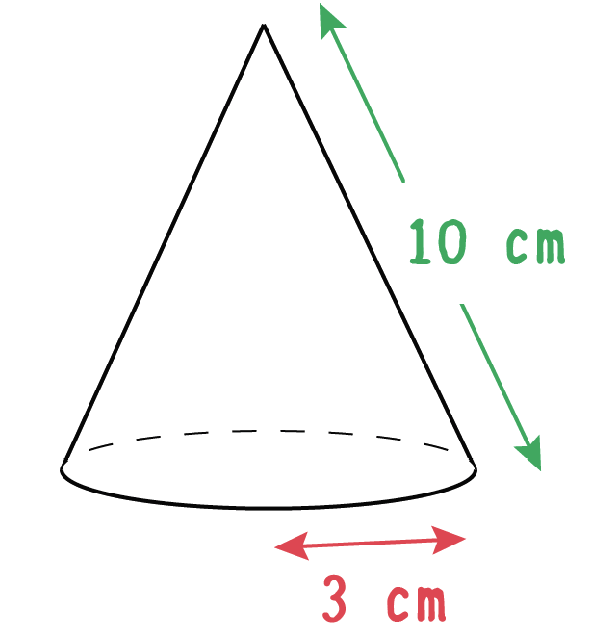
円錐の面積の出し方-円錐の表面積 立体の表面積は各面の面積を求めて,その和を出す。 円錐は底面が円で,側面はおうぎ形である。 側面のおうぎ形の弧の長さは底面の円周の長さに等しい。 底面の半径3cm, 母線の長さ10cmの円錐の表面積を求めよ。 10cm 3cm 10cm 3cm おうぎ形 円 見取図 展開図 円錐を展開すると底ワイズアップ!郡山家庭教師学院です。 円錐の表面積を出すには、 円錐の側面積と底面積を計算して、足さないといけません。 普通は、展開図から側面の中心角の角度を計算して
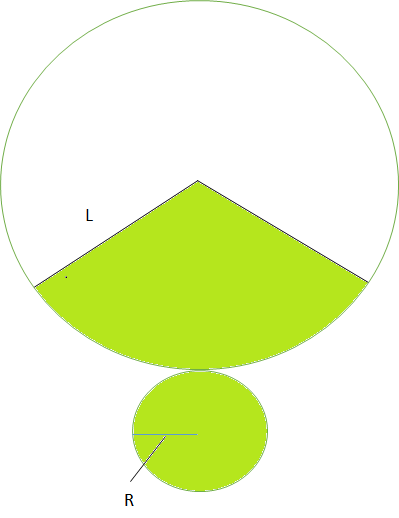



中学数学 円錐と扇形の面積を求める2つの公式 偏差値40プログラマー
底面積 は,半径5cmの円の面積なので, \pi×5^2=25\pi (cm^2) π × 52 = 25π(cm2) 高さ は9cmなので, (底面積)× (高さ)= (体積) より, 25\pi×9=\underline {225\pi (cm^3)} 25π × 9 = 225π(cm3)動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru そのあとに、円錐bの表面積をいつも通り計算してやればいい 成歩 より 19年12月28日 1102 am 体積が一定で、表面積が最小の円柱にしたい場合の半径と高さの比をわかりやすく解説してください。 質問する コメントをキャンセル コメント 名前 知りたいことを検索! 人気記事
『円錐の表面積の求め方』 で悩んでいる方は ↓こちらをご参照ください↓ めっちゃ簡単!?円錐の体積の求め方を解説 おそらく、この記事を見ているほとんどの人が ・解けなかった人 ・解けたけど時間がかかった人 だと思います。 しかしながら、 ある公式を活用することによって、 こ スーちゃん 円すいの体積は円柱の3分の1ってならったよ森羅万象博士 三角すいや四角すいも3分の1になるね。なんでだろう。スーちゃん えっ 円錐の特徴 円錐の特徴は次の二つです 中学数学円錐の側面積の求め方と公式図でわかる! 中学数学が秒でわかる!6枚のカードの同時確率入試レベル 中学数学円柱の表面積の求め方・計算方法ロールケーキでわかる 二等辺三角形の角度を利用した難問・良問
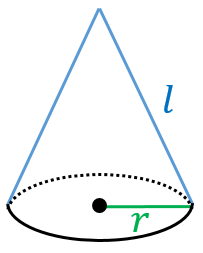
円錐の表面積 底面の半径が r ,母線の長さが R の円錐の表面積を求めるには,右図のように展開図で考え,底面積=円と側面積=扇形の面積を各々求めて加えるとよい. 底面は半径 r の円だから,その面積は πr 2 (1) 側面の扇形の面積を求めるためには,その中心角を求めることが重要に問題図の円錐の体積を求めなさい。 錐の体積 → $\textcolor{blue}{底面積×高さ×\frac{1}{3}}$ $\textcolor{blue}{\rm {V=\frac{1}{3}S}h}$ 円錐の底面は円なので、底面積は$3×3×π=\textcolor{blue}{9π}$ 高さは $\textcolor{blue}{4\rm cm}$ よって、体積は $9π × 4 \rm {cm} ×\frac{1}{3}=\textcolor{red}{12π \rm cm^3}$ ※体積を求めるとき円錐台の側面積を求めたかったから。 ご意見・ご感想 円周率をπと表示できるようになるとありがたいなあと思います。 6 1336 40歳代 / 自営業 / 非常に役に立った / 使用目的 植木鉢に使う培養土の計算 ご意見・ご感想 底面と高さで積分すればいいと思ったのですが、もう思い出せ




円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張
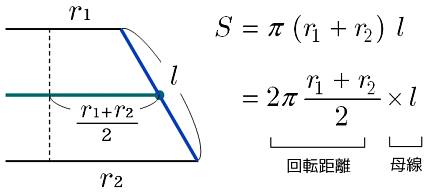



初等幾何 円錐台の側面積を求める 大人が学び直す数学
円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S7 立体の体積と表面積 143 右の図の円錐について,次の問いに答えよ。 ⑴ 底面積を求めよ。 ⑵ 側面の扇形の中心角を求めよ。 ⑶ 側面積を求めよ。 ⑷ 表面積を求めよ。 学基本学習の基本 34 円錐の体積と表面積 問題1 右の図の円錐の体積を求めよ。円錐の表面積を求めますが、展開図ですね。 円錐の展開図は扇形と円となります。 表面積は、扇形の面積と、底面の円の面積を足すだけです。 扇形の面積は普通に求めれば、中心角が\(\,150°\,\)と分かっているので \(\hspace{10pt}\displaystyle \pi\times (12)^2\times \frac{150}{360}\\ \displaystyle =\pi\times (12)^2




中学数学の裏技 円錐の表面積を 10秒 で求める方法 Tara Blog




中学数学 円錐と扇形の面積を求める2つの公式 偏差値40プログラマー
円錐の体積=底面積×高さ÷3なので 答え 096cm³ スポンサードリンク 問題③ 体積が1570cm³である次の円錐の高さを求めましょう。 (円周率は314とします。) 《円錐の高さの求め方》 円錐の体積=底面積×円錐の高さ÷3であることから円錐の側面積と中心角を一瞬で求めてしまう裏ワザ公式です! まぁ、受験ではほとんどの人がこの裏ワザ公式を利用することになると思います。 だって、めっちゃくちゃ簡単だから。 そんな裏ワザ公式とは 母線と半径の長さを利用して $$(側面積)=(母線)\times(半径)\times \pi$$ $$(中心角)=\frac面積比!台形の面積比問題を解説! 円錐の体積比を解説! ←今回の記事 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! 頑張っているのに思うように成績が上がらず、 「このままだと本番で数学60点が厳しいかも」 と不安に感じているあなた。 もしかして、 このような




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
次の錐の表面積を求めよ。 円錐 3cm 10cm 正四角錐 8cm cm pdfファイル 解説ページに解説がない問題で、解説をご希望の場合はリクエストを送信してください。 解説リクエスト 解説リクエストフォーム 問題名 問題番号 mail コメント 空間図形 要点 平面や直線の位置関係 立体の体積 立体の直円錐の表面積 円の面積は、半径×半径×314で求められます。 扇形の面積は、母線×母線×314× (中心角÷360)です。 扇形の面積は、10×10×314× (216÷360)=14c㎡です。球の体積と表面積の公式について まずは証明の前に,球の表面積と体積に関して認識しておくべきことを整理しておきました。 以下の語呂合わせで覚える方法が有名です: 球の表面積: 4 π r 2 4\pi r^2 4πr2 →「心配アール二乗」 球の体積: 4 3 π r 3




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト



円錐の表面積を超簡単に出す裏ワザ公式 個太郎塾
表面積② 円錐の表面積 円錐の展開図 円錐の場合も、円柱と同じように展開図を書いて考えます。円錐の展開図は、底面の部分の円と、側面の部分のおうぎ形の組み合わせになります。 特に注目するのは、底面の円周(上の図の赤い部分)と、側面のおうぎ形の弧(上の図の緑の部分)は積分を用いた証明 二つ目の説明です。数学2の知識が必要になります。積分を使って V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h を証明します。 底面積の形によらない(円錐でも三角錐でも四角錐でも適用可能)証明方法です。 円錐 円錐(えんすい,英 cone)とは,円を底面として持つ錐(きり)状にとがった立体のことである‥. Wikipedia先生によると円錐とはこのような立体のことらしいです. 今日は円錐についてのブログです. 表面積を求める公式 S = r π (r m) S = r π (r m) 母線をm, 半径をr, 高さをh




三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ



円錐の側面積の求め方が分かりません 図のような底面の半径が2cm 母線 Yahoo 知恵袋
Keisanより 長径a,短径bの楕円の面積S=πab、半径rの円の面積はS=πr 2 ですので、直円錐の体積の半径rに開平√ (a*b)を計算して代入すれば、楕円錐の体積が求まります。 5 2338 男 / 歳未満 / 学生 / 役に立った / 使用目的 これからの数学との戦い ご よく知られているように、円錐の体積は 1 3πR2h 1 3 π R 2 h 円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱の体積を求めなさい。ただし、円周率はπとする。 まず、「 柱」の




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
円錐の表面積は上の公式を覚えておけば、すっごく簡単に解くことができちゃいます。 学校では教えてくれないこともあるので、読者のみなさまはコッソリと覚えて使っていきましょうw 次の章では、学校で学習する円錐の基本的な考え方について解説していくよ! 簡単なやり方だけでな円錐の底面積は、円柱の底面積と同じです。円の面積を求めれば良いですね。下記の通りです。 円錐の底面積=5×5×314=785cm 2 四角錐の底面積 四角錐の底面積は、四角柱の底面積と同じ計算です。 四角錐の底面積=(35)÷2×6=24cm 2 三角錐の底面積 三角錐の底面積は三角柱の底面積と計算円錐の側面積 数学・算数のq&A 解決済みOkwave みなさんこんにちは!




現役塾講師直伝 円錐の表面積を求める 裏技 Kouの学び部屋




円錐台 Wikipedia
半径4cm・高さ6cmの円柱 ※円周率を314とした場合 円の面積=4cm×4cm×314=5024cm 2 円の円周=4cm×2×314=2512cm 側面の面積=6cm×2512cm=cm 2 円柱の面積=5024cm 2 5024cm 2 cm 2 =2512cm 2 ※円周率をπとした場合T:高さが同じ三角錐は底面積を合計できるから、円錐の体積は円柱の1/3となる。 s:それはわかったけど、どうして1/2でなくて1/3になるのかがわからない。 5、1/2でなくて、1/3になる理由 t:1/3の意味か。これは難しい質問だ。例えば、 三角形の面積=四角×1/2 三角錐体の体積=四角円錐の体積(Volume) S 底面の面積 h 高さ(height) π 円周率(= 314) r 底面の円の半径(radius) この公式に出てくる 1/3 って何?という疑問を持つ方が多いと思います。その答えは高校2年生で「積分」の勉強をすることで得られます。 積分って何?と興味を持ってくれた方のために、計




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学
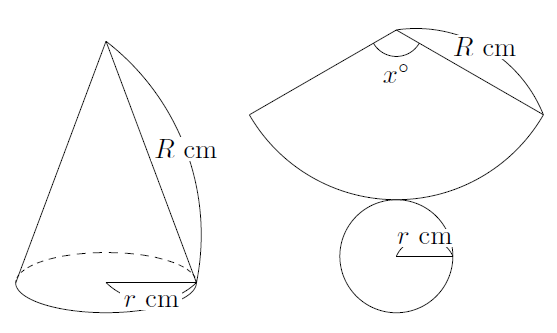



角錐 円錐の表面積 まなびの学園
円錐の微小面積を教えて下さい。 球の微小面積はdSは、 R^2 sinθ dθ dR で表されます。 一方で、円錐の側表面の微小面積はどういう式で表されますか? 検索などして調べたのですが、分かりませんでした。 どなたか教えて下さい。角錐・円錐の体積 = 底面積 × 高さ × 1 3 このやり方では、ちょっとした方程式も出てくるので、早い方でも秒、ゆっくり解くと1分かかることもあるでしょう。 入試本番では、それほど時間をかけてはいられません。 ここで秒殺テクニックの紹介です。 結論からいうと、円すいを開いた時に




円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




円錐の表面積 あんず学習塾のメモ 図表置き場
円錐の側面積の公式 まずは、公式だけ図でさっと確認するよ つぎに、円錐の特徴を確認して、そのあとに側面積を求めていくよ 円錐の特徴 円錐の特徴は主に次の二つだよ 円錐は小さな円と大きな扇で成り立つ;




この円錐の表面積の求め方を教えてください Clear



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典




円錐の表面積を 公式を使って求める チーム エン




中3 三角形の相似 円錐の体積比 日本語版 Youtube




円錐の体積ってなんであの公式なの Webty Staff Blog




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun



図形 円錐の側面積の求め方 名古屋市北区の学習塾は思考力を育む 泰成スクール



Studydoctor円錐の表面積の求め方 中学1年数学 Studydoctor




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
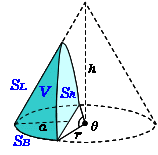



一部が欠けた直円錐の体積 高精度計算サイト




公式を図解 すい体の体積 円すいの表面積の求め方
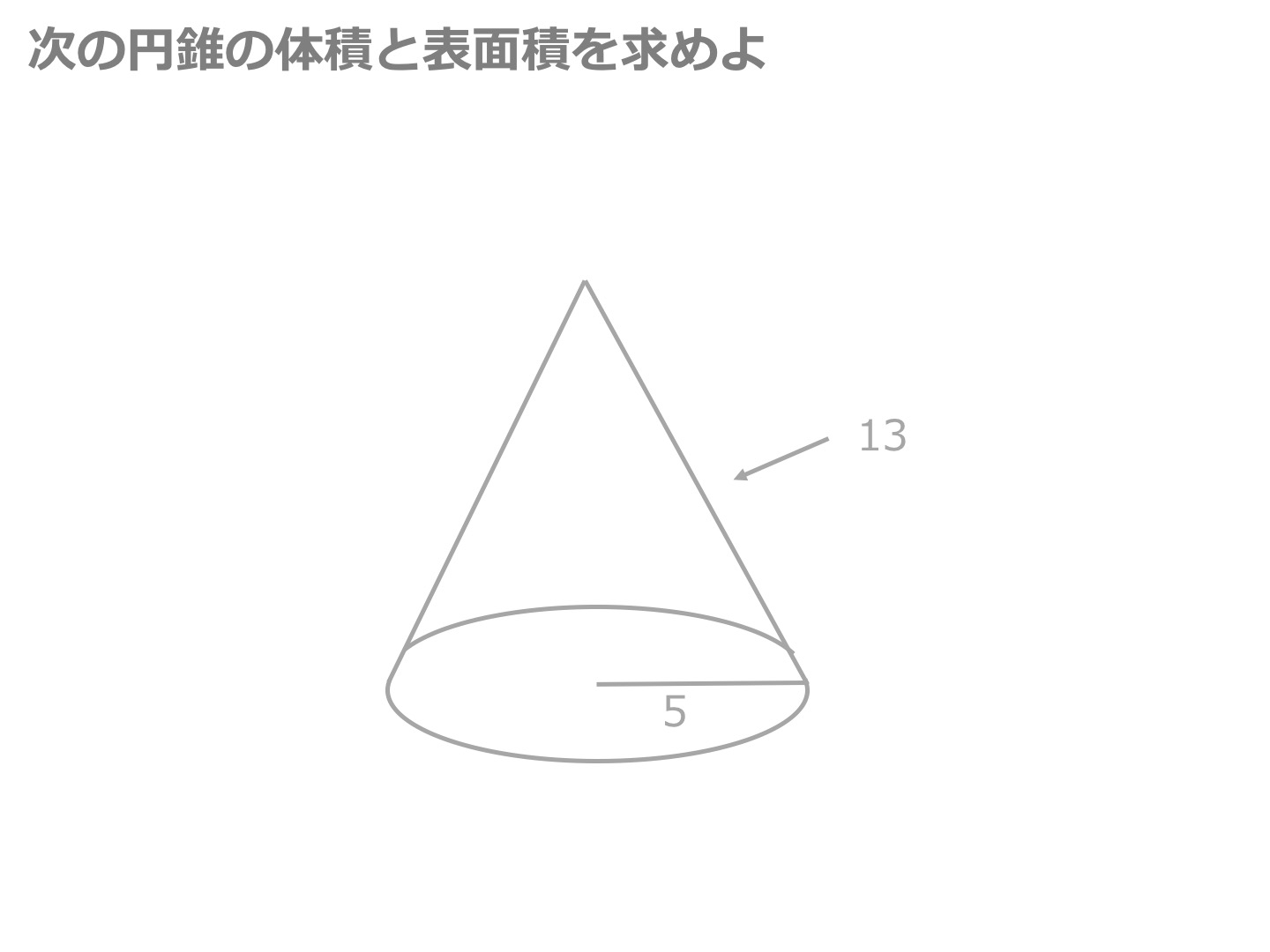



3分でわかる 円錐の体積 表面積の求め方 合格サプリ
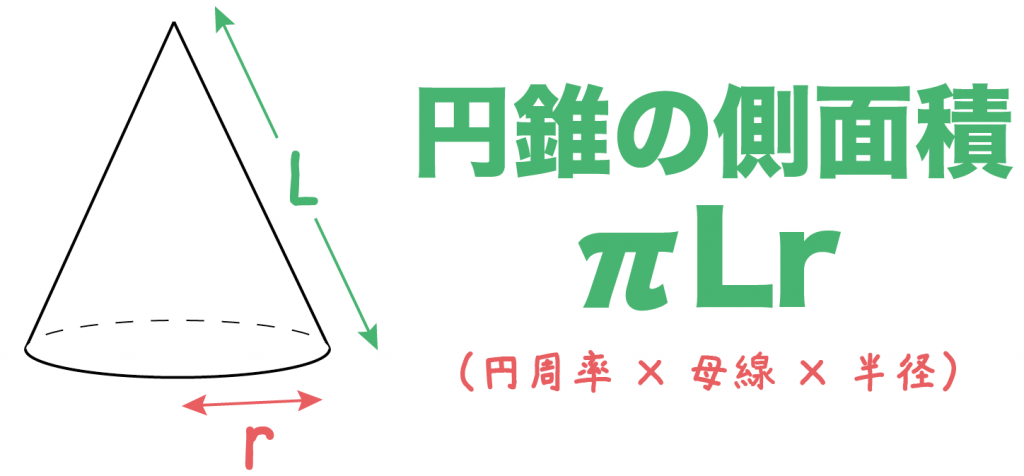



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




公式を図解 すい体の体積 円すいの表面積の求め方



円錐の側面積の求め方 インターネット家庭教師のアスミラ




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




裏ワザ公式 円すいの側面積を一瞬で求める方法 Youtube




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




中学1年生 数学 無料問題集 円すいの表面積 おかわりドリル




3分でわかる 円錐の体積 表面積の求め方 合格サプリ




高校入試対策数学 円錐に関する対策問題 Pikuu
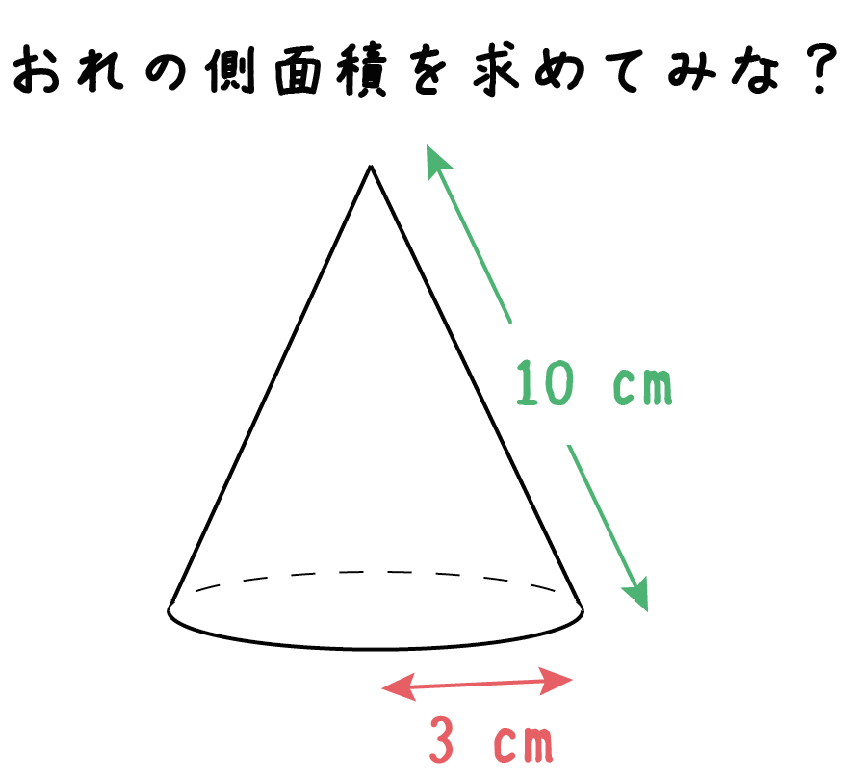



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円すいの展開図 側面積の求め方 公式を使って15秒で解こう




円錐の表面積の求め方 公式と計算例




円錐の表面積 Youtube
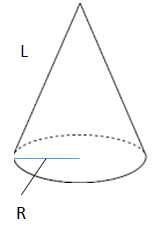



中学数学 円錐と扇形の面積を求める2つの公式 偏差値40プログラマー




円錐の表面積の求め方 公式と計算例



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




高校数学 球に内接する直円錐の体積 側面積の最大値 受験の月
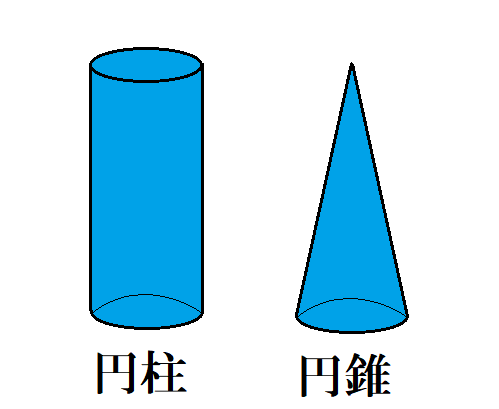



円柱と円錐の違い 表面積や体積 展開図など調べてみたよ ヒデオの情報管理部屋




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




円錐台の体積 側面積 香料ゐっすゐの夢



1




角錐 円錐の体積と表面積の公式 数学fun




投影図から円錐の表面積を求める方法がわかりません 答えと解説を詳しく教えてください Clear




円すい 円錐 の体積の求め方と問題 小学数学 Irohabook



球の表面積 アルキメデスの方法 4の2 セルフ塾のブログ
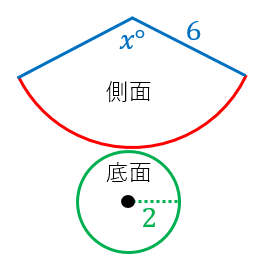



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




円錐の表面積の求め方 You Look Too Cool
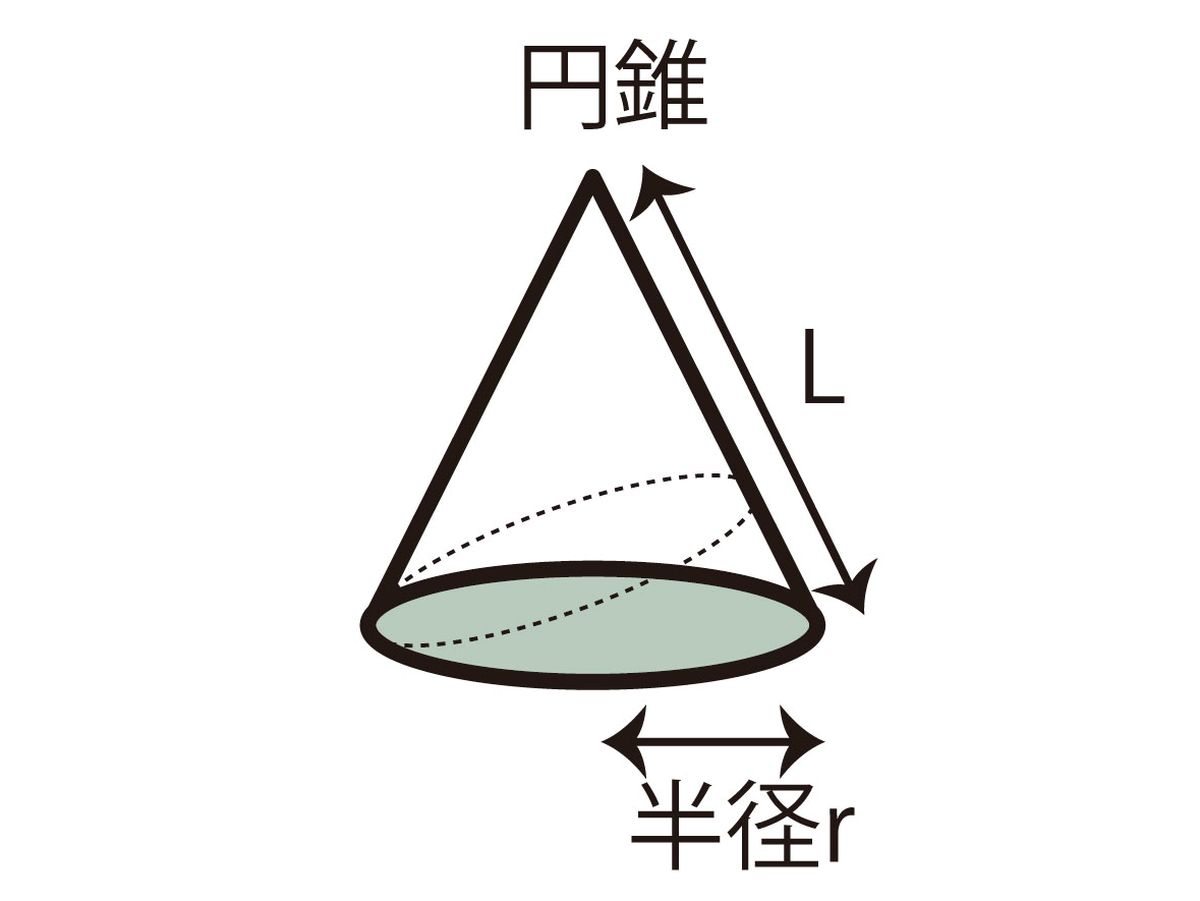



円錐の側面積の公式を理解させる方法 オンライン授業専門塾ファイ




円錐の表面積 簡単な求め方とその理由を解説するぞ 中学数学 理科の学習まとめサイト




公式を図解 すい体の体積 円すいの表面積の求め方



円すい台側面積の公式を導く



1




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
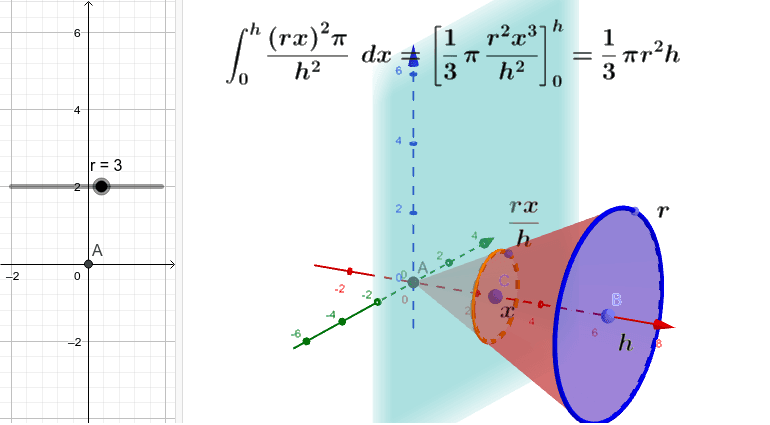



円錐の体積の求め方 Geogebra
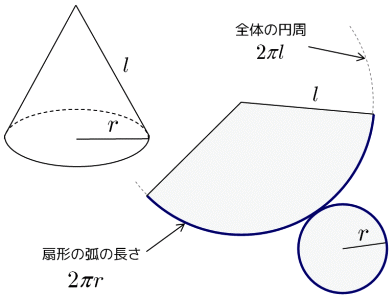



初等幾何 円錐の側面積を求める 大人が学び直す数学




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者



写真の円錐の体積と表面積を求める問題なんですが この答えであっているでしょ Yahoo 知恵袋




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット



6 17 第6章 空間図形立体の表面積と体積 円錐の表面積 ニュージーランド短期留学ダイアリー



1




円錐の側面積 展開図の扇形の中心角 教科書から 身勝手な主張
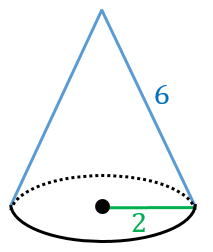



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学



球の半分と円錐を組み合わせた立体です 体積と表面積を求めよ 教え Yahoo 知恵袋




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐台の側面積の 1 1 3 がよくわかりません なぜ2条にするのですか Clear




Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ




中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室




この問題の円錐の底面積の半径の求め方を教えてください Clear




円錐の体積と表面積の求め方 押さえておくべき公式と解法の手順




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室



1



円錐とは 体積 表面積の公式や求め方 受験辞典



中学数学 円すいに関する練習問題
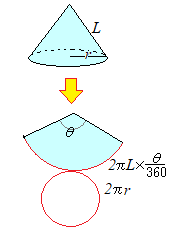



立体の表面積



底面積の求め方は 5分でわかる計算 円柱 円錐 四角柱 三角柱の底面積




円錐の表面積の求め方 公式と計算例




数学でどうしてもわからない問題があります この円錐の表面積を求め 中学校 教えて Goo




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




毎日問題を解こう 27 苦手な数学を簡単に




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



円錐の側面積 中学から数学だいすき
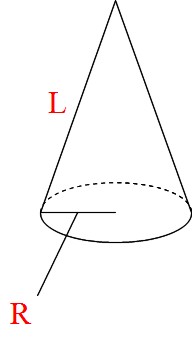



Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ
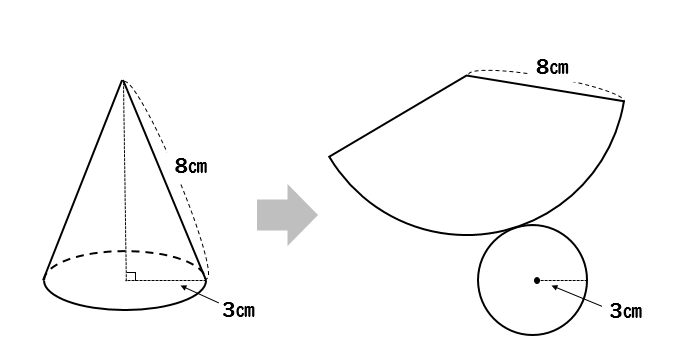



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ



Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ




中学数学 円錐の裏技集 暗算で中心角 側面積 表面積 中1数学 Youtube
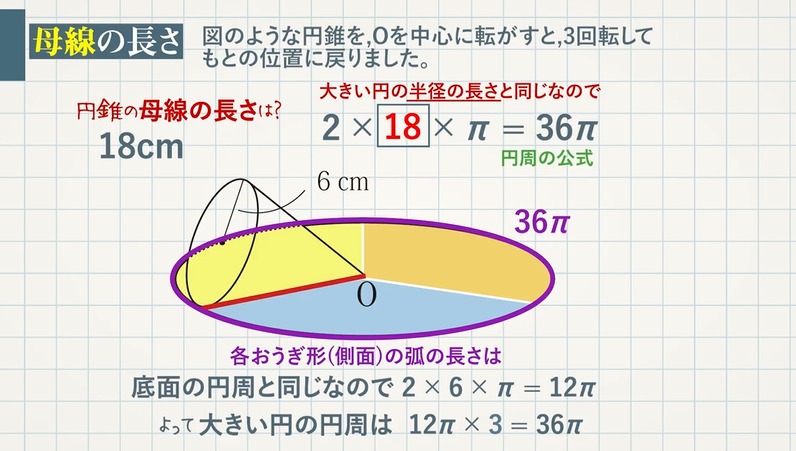



円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者


